Current Status & The Hunt for a Counterexample
As of today, the FLRP remains unsolved. It stands as one of the most significant open problems in universal algebra.
The Prevailing Conjecture
The general consensus among experts is that the answer to the FLRP is no. The conjecture is that there exists at least one finite lattice that cannot be represented as the congruence lattice of any finite algebra. This belief is fueled by the decades-long failure to find a general proof and the immense difficulty in constructing representations for even moderately complex lattices.
Major Obstacles
- Finiteness is tricky: We lack a deep understanding of how the constraint of a finite universe restricts the structure of a congruence lattice.
- Constructions are hard: Methods for building algebras with a prescribed congruence lattice often result in infinite algebras.
- Group theory is hard: The Pálfy-Pudlák equivalence translates FLRP into an equally challenging problem within finite group theory.
Candidate Counterexample: The L7 Lattice
The entire search for a counterexample—a specific finite lattice that would prove the conjecture true—is currently focused on a single, 7-element lattice.
The L7 Lattice
The smallest finite lattice for which representability by a finite algebra is unknown is a 7-element lattice, denoted L7 (discovered by William DeMeo).
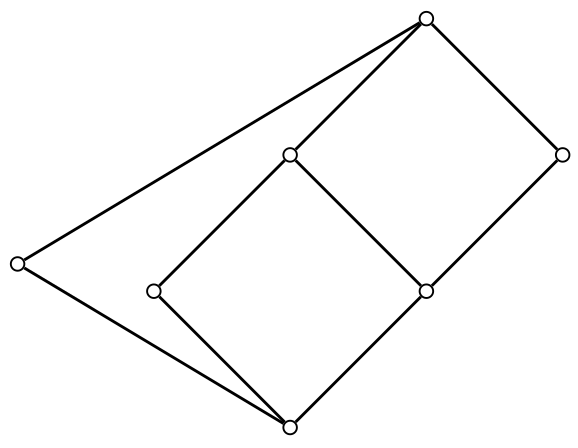
- It is the only 7-element lattice whose status is unresolved.
- All lattices with 6 or fewer elements are known to be representable.
- This makes L7 the critical test case for the entire Finite Lattice Representation Problem.
- Intense effort, including computational searches, has so far failed to produce a representing algebra for L7.
Proving that L7 is not representable would definitively solve the FLRP with a negative answer. Conversely, finding a finite algebra for L7 would constitute an important breakthrough.