Revisiting Enforceable Properties for the Finite Lattice Representation Problem: A Tame Congruence Theory Perspective

This page was created in collaboration with the Gemini 2.5 Pro AI assistant in "Deep Research" mode.

1. The Finite Lattice Representation Problem: Context and Framework

This section establishes the foundational context of the Finite Lattice Representation Problem (FLRP) and meticulously dissects DeMeo's contributions [1], highlighting the mechanisms relevant to the proposed combined strategy.

1.1. Brief Recapitulation of the FLRP and the Pálfy-Pudlák Theorem

The Finite Lattice Representation Problem (FLRP) stands as a central open question in universal algebra, asking for a characterization of those finite lattices that are isomorphic to the congruence lattices of finite algebras.[20] The study of congruence lattices, which encode the homomorphic images and internal symmetries of algebraic structures, is fundamental to understanding the structure of algebras themselves.

A pivotal result connecting this problem to group theory is the Pálfy-Pudlák Theorem.[17] This theorem states two equivalent conditions:

• (A) Every finite lattice is isomorphic to the congruence lattice of some finite algebra \(A\) (denoted \(\mathrm{Con}(A)\)).
• (B) Every finite lattice is isomorphic to an interval in the subgroup lattice of some finite group \(G\) (denoted \([H, G]\), representing the lattice of subgroups of \(G\) containing \(H\) and contained in \(G\)).

The equivalence (A) ⟺ (B) implies that if one can find a finite lattice \(L\) for which it can be proven that no finite group \(G\) exists such that \(L ≅ [H, G]\) for some subgroup \(H\) of \(G\), then it would follow that statement (A) is false, and the FLRP would have a negative answer. This theorem, therefore, transforms a problem in universal algebra and lattice theory into a problem concerning the structure of subgroup lattices of finite groups, providing the primary motivation for the approach detailed in DeMeo.[1] The strategic importance of this connection cannot be overstated, as it opens a pathway to addressing the FLRP through group-theoretic constructions and arguments.

1.2. Core-Free Interval Enforceable (cf-IE) Properties: Definitions and Significance

In [1], building upon the Pálfy-Pudlák theorem [17], DeMeo introduces a classification of group-theoretic properties based on their relationship to lattice intervals. An "interval enforceable (IE)" property \(P\) is a group property for which there exists a finite lattice \(L\) such that if \(G\) is a group with \(L\) isomorphic to an interval \([H, G]\) in its subgroup lattice \(\mathrm{Sub}(G)\), then \(G\) must possess property \(P\).

A more refined and crucial concept for the FLRP is that of core-free interval enforceable (cf-IE) properties. A property \(P\) is cf-IE if there exists a finite lattice \(L\) such that if \(G\) is a group with \(L ≅ [H, G]\) and \(H\) is a core-free subgroup of \(G\) (i.e., \(\mathrm{core}_G(H) = 1\), meaning \(H\) contains no non-trivial normal subgroup of \(G\)), then \(G\) must possess property \(P\).[1]

The core-free condition, \(\mathrm{core}_G(H) = 1\), is of paramount significance. When \(H\) is core-free in \(G\), the group \(G\) admits a faithful permutation representation \(ϕ\) on the set of right cosets \(G/H\). It is a well-established result that the congruence lattice of the algebra \(⟨G/H, ϕ(G)⟩\) (formed by the \(G\)-set \(G/H\) with the action of \(G\)) is isomorphic to the interval \([H, G]\) in \(\mathrm{Sub}(G)\).

This isomorphism is the critical link: it means that a core-free interval \([H, G]\) is the congruence lattice of a specific finite algebra derived directly from the group \(G\) and subgroup \(H\). Consequently, cf-IE properties are group properties that are forced upon \(G\) when a particular lattice \(L\) appears as the congruence lattice of such a \(G\)-set. This directly connects the study of subgroup intervals under the core-free condition to statement (A) of the Pálfy-Pudlák theorem, making cf-IE properties particularly potent tools for investigating the FLRP. Without the core-free assumption, the interval \([H, G]\) might not directly correspond to a congruence lattice of an algebra naturally derived from \(G\) in a way that is immediately relevant to the FLRP as formulated by Pálfy and Pudlák in [17].

DeMeo [1] provides several examples of cf-IE properties. Insolubility is shown to be IE (and therefore cf-IE), while solubility is demonstrated to be not even cf-IE. Other identified cf-IE classes of groups include those that are not alternating or symmetric groups, subdirectly irreducible groups, groups possessing no non-trivial abelian normal subgroups, and groups \(G\) for which the centralizer \(C_G(M)\) is trivial for every non-trivial normal subgroup \(M\) of \(G\). These examples underscore that cf-IE properties can be substantial and non-trivial, offering a way to impose strong structural constraints on groups based on the lattice-theoretic structure of their subgroup intervals.

1.3. Strategic Importance of Thm 3.6 and the Parachute Construction for FLRP

A cornerstone of DeMeo's proposed strategy for the FLRP is Theorem 3.6 of [1]. This theorem establishes further equivalences to statement (B) of the Pálfy-Pudlák theorem (and thus to a positive answer to the FLRP). Among these, statement (C) is particularly relevant:

• (C) For every finite lattice \(L\), for every finite collection \(X_1\), ..., \(X_n\) of cf-IE classes of groups, there exists a finite group \(G ∈ ⋂ \{X_i : 1 ≤ i ≤ n\}\) such that \(L ≅ [H, G]\) for some subgroup \(H\) that is core-free in \(G\).

The strategic implication of Theorem 3.6 (C) is profound: if one could identify a finite collection of cf-IE classes of groups, \(X_1\), ..., \(X_n\), whose intersection is empty (i.e., no finite group can simultaneously possess all these properties), then statement (C) would be false for any choice of \(L\). This, in turn, would imply that statement (B) of the Pálfy-Pudlák theorem is false, leading to a negative resolution of the FLRP. This transforms the FLRP into a concrete group-theoretic problem: the search for a set of mutually incompatible cf-IE properties.

The "parachute lattice" construction (Figure 4 of [1] and reproduced below), denoted \(P(L, L_1, ..., L_n)\), is a key technical device used in proving the equivalence (B) ⟹ (C). This construction involves creating a new lattice P from a given lattice \(L\) and a set of lattices \(L_1\), ..., \(L_n\) (where each \(L_i\) is known to enforce a cf-IE property \(P_i\)). If statement (B) holds, then \(P\) must be representable as a core-free interval \([H, G]\) for some group \(G\). The structure of the parachute lattice then ensures that the sub-intervals within \([H, G]\) corresponding to \(L_i\) are also core-free intervals isomorphic to \(L_i\). Consequently, \(G\) must possess each property \(P_i\), placing \(G\) in the intersection \(⋂ P_i\). The parachute lattice, therefore, serves as a conceptual blueprint for how multiple cf-IE constraints could be simultaneously imposed on a single group \(G\), should the FLRP have a positive answer. The failure to find such a group \(G\), under increasingly restrictive (yet valid) cf-IE conditions, would provide evidence against the FLRP.

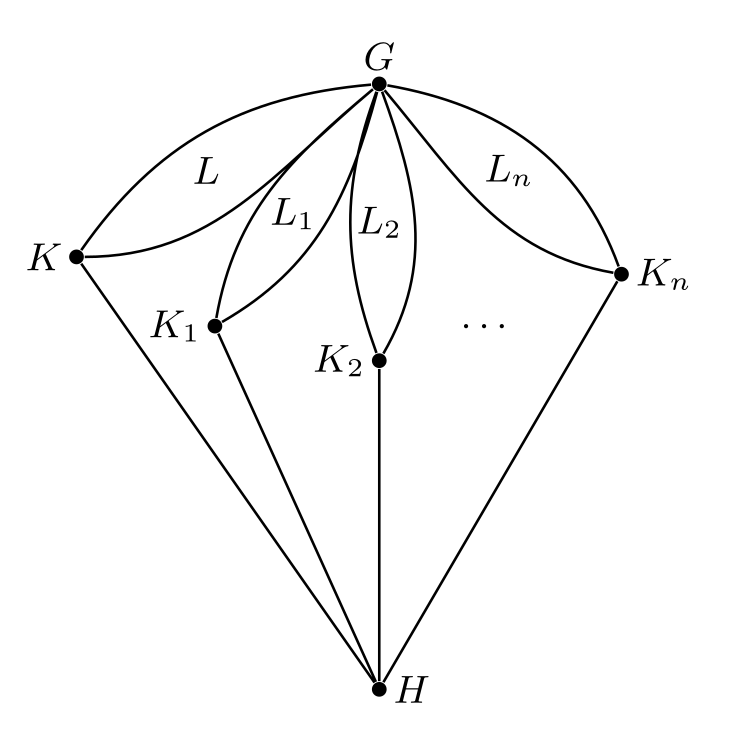
Furthermore, Corollary 3.9 of [1], which follows from the parachute construction logic, states that the conjunction of any finite number of cf-IE properties is itself a cf-IE property. This reinforces the strategy of accumulating multiple cf-IE properties with the aim of reaching a contradiction (an empty intersection).

1.4. Illustrative Example: Insights from the Analysis of \(L_7\)

DeMeo's paper provides a compelling illustration of this strategy through a detailed analysis of a specific seven-element lattice, denoted \(L_7\). (Figure 4 of [1] and reproduced below.) This lattice is notable as it is the smallest for which a congruence lattice representation (\(L_7 ≅ \mathrm{Con}(A)\) for some finite algebra A) is not yet known.[18, 19]

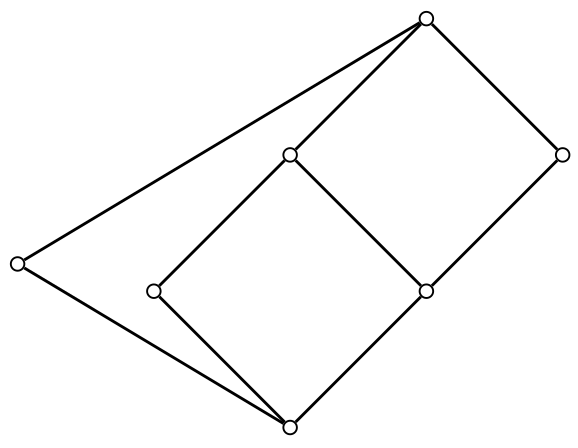
Proposition 4.1 of [1] outlines a set of strong group-theoretic properties that any finite group \(G\) must possess if \(L_7\) is isomorphic to a core-free interval \([H, G]\) in \(\mathrm{Sub}(G)\):

1. \(G\) must be a primitive permutation group (derived from the core-freeness of a maximal subgroup \(K\) corresponding to an element in \(L_7\)).

2. For any non-trivial normal subgroup \(N\) of \(G\), its centralizer \(C_G(N)\) must be trivial.

3. \(G\) can contain no non-trivial abelian normal subgroups (a direct consequence of the trivial centralizer property).

4. \(G\) must be insoluble (also a consequence of the trivial centralizer property for minimal normal subgroups).

5. \(G\) must be subdirectly irreducible (possessing a unique minimal normal subgroup).

6. With the possible exception of at most one maximal subgroup in the interval \([H, G]\), all proper subgroups within this interval must be core-free in \(G\).

This analysis of \(L_7\) serves as a powerful proof-of-concept for DeMeo's general strategy. It demonstrates that even a relatively small and specific lattice structure can impose a formidable list of cf-IE properties on any group \(G\) that might represent it as a core-free interval. These derived properties significantly narrow the class of potential candidate groups \(G\). The internal structure of the lattice \(L_7\) itself---its specific configuration of meets, joins, and elements like the non-modular element \(K\)---is what drives the deduction of these group properties, often in conjunction with group-theoretic tools like Dedekind's rule and Lemma 3.5 (concerning permuting subgroups).[1] This highlights that a deep understanding of how lattice-theoretic features translate into cf-IE properties is essential. The techniques employed in the \(L_7\) analysis may prove adaptable when considering new enforceable properties derived from Tame Congruence Theory.

2. Tame Congruence Theory: A Structural Lens for Finite Algebras

Tame Congruence Theory (TCT), primarily developed by David Hobby and Ralph McKenzie [2], offers a sophisticated framework for analyzing the structure of finite algebras by examining the local behavior of their congruence lattices. This theory provides the conceptual tools for potentially defining new and powerful enforceable properties relevant to the FLRP.

2.1. Fundamental Concepts.

The fundamental concepts of TCT are the following:

• minimal algebras;
• the five TCT types;
• (α, β)-minimal sets (traces, body, tail);
• labeled congruence lattices.

At the heart of TCT is the analysis of prime quotients α ≺ β (meaning α is covered by β) in the congruence lattice \(\mathrm{Con}(A)\) of a finite algebra \(A\). The local behavior of the algebra in the "vicinity" of such a quotient is captured by (α, β)-minimal sets.

An (α, β)-minimal set \(U\) is the range of an idempotent unary polynomial \(e\) of \(A\), minimal with respect to the property that the restrictions \(α∣_U\) and \(β∣_U\) are different.[3]

Within an (α, β)-minimal set \(U\), certain \(β∣_U\)-classes, known as traces, are particularly important; these are the \(β∣_U\)-classes that are not contained in a single \(α∣_U\)​-class. The union of all traces in \(U\) forms the body \(B\) of \(U\). The remaining part, \(T = U - B\), is called the tail.[3] TCT provides a rich structural understanding of the body, while the tail is considered less structured or "wild" from the theory's perspective.[3]

A key discovery of TCT is that the algebra \(A∣_N\) (the operations of \(A\) restricted to \(N\), where \(N\) is a trace), when factored by the restricted congruence \(α∣_N\), is polynomially equivalent to one of precisely five types of minimal algebras.[2]

A minimal algebra \(M\) is a finite algebra with at least two elements in which every non-constant unary polynomial is a permutation of its domain.[5]

The five TCT types (of minimal algebras) are the following:

1. Type 1 (Unary): pol-equiv to a \(G\)-set.
2. Type 2 (Affine): pol-equiv to a vector space over a finite field.
3. Type 3 (Boolean): pol-equiv to the two-element Boolean algebra.
4. Type 4 (Lattice): pol-equiv to the two-element lattice.
5. Type 5 (Semilattice): pol-equiv to the two-element semilattice.

This classification allows each prime quotient α ≺ β in \(\mathrm{Con}(A)\) to be assigned one of these five types, transforming \(\mathrm{Con}(A)\) into a labeled congruence lattice.[2] This labeling provides a "local flavor" for the algebra at each prime quotient.

The connection to DeMeo's framework arises when considering the algebra \(A_G = ⟨G/H, ϕ(G)⟩\), whose congruence lattice is isomorphic to the interval \([H, G]\) when \(H\) is core-free.[1] Thus, a TCT analysis of a lattice \(L\), when \(L ≅ [H, G]\), is effectively a TCT analysis of \(\mathrm{Con}(A_G)\). The TCT types observed in \(L\) (as \(\mathrm{Con}(A_G)\)) become fundamental characteristics. The challenge and opportunity lie in translating these type-dependent properties of \(A_G\) back into group-theoretic properties of \(G\) that can be classified as cf-IE.

Table 1. Summary of the Five TCT Types of Minimal Algebras. This table summarizes the five types of minimal algebras central to TCT, their characterizing algebraic structures, and the nature of their polynomial clones when induced on a trace \(N\) for a prime quotient typ(α, β).

Type	Name	Characterizing Algebraic Structure	Nature of Poly Clone on Trace \(N\) (\(A∣_N/α∣_N\))
1	Unary	Permutation group on a set	All operations are essentially unary (permutations or constants), or can be simulated by such.
2	Affine	Vector space over a finite field	All operations are affine transformations (linear combinations + translations).
3	Boolean	Two-element Boolean algebra	All operations are those of a Boolean algebra (e.g., join, meet, complement).
4	Lattice	Two-element lattice	All operations are those of a lattice (e.g., join, meet).
5	Semilattice	Two-element semilattice	All operations are those of a semilattice (e.g., join or meet).

Table 1 provides a concise reference for the fundamental TCT classification, highlighting the core algebraic structure and polynomial characteristics associated with each local type. This is crucial for understanding how TCT might define enforceable properties for \(A_G\), which could then translate to properties of \(G\). This information is synthesized from multiple sources.[2]

2.2. Connecting Local Structure to Global Properties: TCT Types, Malt'sev Conditions, Congruence Identities, Solvability, and Abelianness

TCT reveals deep connections between the local types present in \(\mathrm{Con}(A)\) and global properties of the algebra \(A\) and the variety \(V(A)\) it generates. A variety is a class of algebras closed under homomorphic images, subalgebras, and direct products. (Alternatively, and equivalently according to Birkhoff's HSP Theorem, a variety is an equational class of algebras.)

Omitting Types and Malt'sev Conditions. A particularly powerful aspect of TCT is the characterization of varieties that omit certain sets of types. Such omissions are often equivalent to the variety satisfying specific Malt'sev conditions, which are sets of term identities.[6] For locally finite varieties:

• Omitting type 1 (unary type) is equivalent to the variety being a Taylor variety, i.e., possessing a Taylor term. A Taylor term is an idempotent term \(t(x_1, ..., x_n)\) such that for each \(i ∈ \{1, ..., n\}\),

\[t(x, ..., x, y, x, ..., x) = t(x, ..., x, z, x, ..., x)\]

holds if \(y\) and \(z\) are in the \(i\)-th position and all other variables are \(x\).[6]

• Omitting types {1, 5} (unary and semilattice types) is equivalent to the variety satisfying a non-trivial congruence identity and possessing a Hobby-McKenzie term.[6]
• Omitting types {1, 2} (unary and affine types) is equivalent to the variety being congruence meet-semidistributive (SD(∧)).[6]
• Omitting types {1, 2, 5} (unary, affine, and semilattice types) is equivalent to the variety being congruence join-semidistributive (SD(∨)).[6]
• A variety is congruence modular if and only if its type set is contained in {2, 3, 4} and all its minimal sets have empty tails.[3]
• A variety is congruence distributive if and only if its type set is contained in {3, 4} and all its minimal sets have empty tails.[10]

These equivalences provide a pathway: if the structure of a lattice \(L\) (as \(\mathrm{Con}(A_G)\)) forces the omission or presence of certain TCT types in \(A_G\), then \(A_G\) (or \(V(A_G)\)) must satisfy corresponding strong algebraic conditions. The primary challenge, then, is to translate these algebraic properties of \(A_G\) (e.g., "possesses a Taylor term") into meaningful group-theoretic properties of \(G\) that can be shown to be cf-IE.

Solvability and Abelianness. Commutator theory for congruences defines notions of solvable and abelian congruences. A prime quotient α ≺ β is abelian if the commutator [β, β] is less than or equal to α. An interval \(I[δ, θ]\) is solvable if it has a finite chain of congruences \(δ = γ_0 ≺ γ_1 ≺ ⋯ ≺ γ_k = θ\) such that each factor \(I[γ_i, γ_{i+1}]\) is abelian.[12]

• Prime quotients of type 2 (affine) are always abelian.[2]
• Prime quotients of type 1 (unary) can be either abelian or non-abelian.[2]
• If an interval \(I[δ, θ]\) is solvable, then all its prime factors must be of type 1 or type 2 [2 (Theorem 7.12)]. This connection is significant because if a lattice \(L\), when represented as \(\mathrm{Con}(A_G)\), forces certain intervals to be solvable or certain quotients to be abelian (or non-abelian), this imposes strict TCT type constraints on \(\mathrm{Con}(A_G)\).

2.3. Tameness and the Significance of Empty Tails in Minimal Sets

The term "tame" in TCT broadly refers to the well-behaved, structured nature of local polynomial operations, particularly on the body of an (α, β)-minimal set \(U\). TCT provides extensive information about the structure induced on the body \(B\). In contrast, the tail \(T = U - B\) is often described as "wild," meaning TCT offers very little structural insight into it.[3]

The condition that minimal sets have empty tails (\(T = ∅\), so \(U = B\)) is highly significant. When tails are empty, the local structure is fully "tame," and the analytical power of TCT can be most effectively applied. The presence of non-empty tails, especially for types 1 or 5, is intrinsically linked to failures of congruence modularity. For instance, if a minimal set of type \(i ∈ \{2, 3, 4, 5\}\) has a non-empty tail, it forces the existence of a pentagonal sublattice N5 (a hallmark of non-modularity) of type \(i\) in the congruence lattice of some subalgebra of \(A^2\). Contrapositively, strong conditions on the labeled congruence lattice, such as the absence of pentagons, can force tails to be empty.[3]

For a locally finite variety \(V\) to be congruence modular, two conditions must be met: its type set must be restricted to {2, 3, 4} (i.e., types 1 and 5 must be omitted), AND all minimal sets associated with these types must have empty tails.[3] The "empty tails" condition is thus a critical component of "tameness" in the context of well-behaved varieties like congruence modular ones.

If a lattice \(L\), interpreted as \(\mathrm{Con}(A_G)\), were to force \(A_G\) to have minimal sets with non-empty tails of type 1 or 5, this would indicate a certain "wildness" in \(A_G\) and imply that \(V(A_G)\) is not congruence modular. Such "wildness," if translatable into a group-theoretic property, could be a candidate for a cf-IE property. The challenge remains in formalizing "wildness" (e.g., non-empty tails of specific types) as an algebraic property of \(A_G\) that subsequently translates into a cf-IE group property of \(G\).

3. Defining Enforceable Properties via Tame Congruence Theory

This section explores concrete ways TCT concepts can be harnessed to define new cf-IE group properties, focusing on the crucial step of translating properties of \(\mathrm{Con}(A_G)\) or the algebra \(A_G\) itself into properties of the group \(G\).

3.1. Leveraging TCT Types: Proposing cf-IE properties based on the presence or omission of specific TCT types or type configurations in \(\mathrm{Con}(A_G)\).

A primary avenue for defining new enforceable properties through TCT involves the set of types present in \(\mathrm{Con}(A_G)\) (which is isomorphic to the interval \(L ≅ [H, G]\) when \(H\) is core-free).

Properties Based on Type Omission. If a lattice \(L\), by its structure, forces any algebra \(A\) for which \(\mathrm{Con}(A) ≅ L\) to omit certain TCT types from its type set (or from the type set of the variety \(V(A)\) it generates), this leads to strong algebraic consequences. For instance:

• If \(L\) forces \(V(A_G)\) to omit type 1 (unary type), then \(A_G\) must possess a Taylor term, and \(V(A_G)\) is a Taylor variety.[6]

• If \(L\) forces \(V(A_G)\) to omit types {1,5} (unary and semilattice types), then \(A_G\) must satisfy a non-trivial congruence identity and possess a Hobby-McKenzie term.[6] The critical step is then to determine if "\(G\) is a group such that \(A_G\) has a Taylor term (or satisfies a given congruence identity)" can be established as a cf-IE property of \(G\), meaning it is enforceable by some (potentially different) lattice \(L′\). This translation from an algebraic property of \(A_G\) to a cf-IE group property of \(G\) represents a significant theoretical challenge.

Properties Based on Type Presence. Conversely, if the structure of \(L\) forces \(\mathrm{Con}(A_G)\) to exhibit certain TCT types, this can also lead to enforceable properties. For example, if \(L\) is a non-modular lattice, then \(\mathrm{Con}(A_G)\) must be non-modular. In locally finite varieties, non-modular congruence lattices necessitate the presence of TCT types 1 or 5 [2 (Corollary 5.20)]. Thus, if a non-modular lattice \(Lₙₘ\) enforces the property "\(A_G\) admits type 1 or type 5," then "\(G\) is a group such that \(A_G\) admits type 1 or 5 when \(Lₙₘ ≅ [H, G]\)" could be a candidate cf-IE property.

The "empty tails" condition is an important qualifier. Properties like "\(V(A_G)\) omits type 1 AND has empty tails for all its minimal sets" would be stronger and more directly related to conditions like congruence modularity.[2]

The translation hurdle remains: how does an algebraic property of \(A_G\) (like "\(V(A_G)\) is congruence modular") translate to a cf-IE group property of \(G\)?

3.2. Exploiting Geometric Constraints in Labeled Congruence Lattices

The geometric configuration of prime quotients within \(\mathrm{Con}(A) ≅ L\) imposes constraints on their TCT type labels.

• Perspectivity and Projectivity. Two prime quotients \(I_1​ = I[α, β]\) and \(I_2​ = I[γ, δ]\) in \(\mathrm{Con}(A)\) are perspective if they are opposite sides of a diamond (M3) or a pentagon (N5) (in which case, \(α = β ∧ γ\) and \(δ = β ∨ γ\)). Projectivity is a sequence of perspectivities. A fundamental result in TCT (often detailed in Chapter 6 of Hobby & McKenzie, e.g., Lemmas 6.2--6.6) is that if two prime quotients are projective, they must have the same TCT type, provided certain conditions hold (e.g., the projectivity avoids type 1 quotients or the lattice is modular).[2] This "type consistency under projectivity" is a powerful constraint.
• N5 (Pentagon) Subconfigurations. If \(L ≅ \mathrm{Con}(A_G)\) contains an N5 sublattice, then \(\mathrm{Con}(A_G)\) is non-modular. This forces \(V(A_G)\) to admit TCT types 1 or 5. The prime quotients forming the N5 configuration will be labeled accordingly, with at least one of them (often the critical quotient) being of type 1 or 5 [2 (Corollary 5.20), 15].
• M3 (Diamond) Subconfigurations. If \(L ≅ \mathrm{Con}(A_G)\) contains an M3 sublattice, then \(\mathrm{Con}(A_G)\) is non-distributive. If \(V(A_G)\) were congruence distributive, it would omit types 1, 2, and 5. Therefore, the presence of an M3 implies that \(V(A_G)\) is not congruence distributive, and thus must admit type 1, 2, or 5. Furthermore, if \(\mathrm{Con}(A_G)\) is modular (which M3 itself is), types 1 and 5 are omitted from modular intervals unless specific conditions apply (related to solvability).

A variety is congruence meet-semidistributive (SD(∧)) if and only if M3 is not embeddable in \(\mathrm{Con}(A)\) for any \(A ∈ V\); SD(∧) is equivalent to omitting types {1, 2}.[8] Thus, the presence of an M3 implies the variety is not SD(∧), meaning it must admit type 1 or type 2. If the interval containing M3 is known to be modular, this would point towards type 2. The three covering quotients forming the "sides" of an M3 in a modular lattice are perspective and thus must have the same type (from {2, 3, 4}).

These geometric constraints offer a direct mechanism for \(L\) to enforce TCT types on \(A_G\). For example, if \(L_{\mathrm{target}}\) contains an N5 configuration, then any group \(G\) representing \(L_{\mathrm{target}}\) as \(\mathrm{Con}(A_G)\) must be such that \(A_G\) admits type 1 or 5. This admission of "wilder" types becomes an algebraic property of \(A_G\), which then needs to be translated into a cf-IE group property of \(G\). The analysis of \(L_7\) in DeMeo's paper implicitly uses such geometric reasoning; for instance, its non-modularity contributes to the derived properties of \(G\).

3.3. The Role of Solvable/Abelian Congruence Quotients and their TCT Type Correlates

The notions of solvability and abelianness for congruence quotients are deeply connected to TCT types.

• A prime quotient \(I[α, β]\) is abelian if the commutator [β, β] ≤ α. All type 2 (affine) quotients are abelian. Type 1 (unary) quotients can be either abelian or non-abelian.[2]. Types 3, 4, and 5 are non-abelian.

• An interval \(I[δ, θ]\) is solvable if it has a composition series where each prime factor is abelian. Consequently, if an interval is solvable, all its prime factors must be of type 1 or type 2. [2 (Theorem 7.12)]

If the structure of a lattice \(L\) (when \(L ≅ \mathrm{Con}(A_G)\)) forces certain intervals in \(\mathrm{Con}(A_G)\) to be solvable, or certain prime quotients to be abelian (or non-abelian), then this imposes strict constraints on the TCT types present. For instance, if \(L\) forces a prime quotient in \(\mathrm{Con}(A_G)\) to be non-abelian, then that quotient cannot be of type 2 and, if type 1, must be a non-abelian type 1. DeMeo's result that insolubility of \(G\) is IE [1] is an example of how such properties might connect; if \(A_G\) having only solvable congruence quotients implied \(G\) is solvable, then a lattice \(L\) forcing a non-solvable quotient in \(\mathrm{Con}(A_G)\) might enforce \(G\)'s insolubility. This link between the TCT commutator and group-theoretic solvability/nilpotency is a promising area for defining cf-IE properties.

4. Assessing the Combined Strategy: Synergies, Potential, and Challenges

This section critically evaluates the feasibility and potential impact of the combined DeMeo-TCT approach to the FLRP.

4.1. Potential for Progress: The Path to Contradiction

The central strategy, as illuminated by DeMeo's Theorem 3.6 [1], is to identify a collection of cf-IE group properties whose intersection is empty. If such a collection \(\{P_j\}\) exists, then the FLRP would have a negative answer. Tame Congruence Theory offers a powerful new toolkit to define candidate cf-IE properties.

The synergy unfolds as follows:

1. DeMeo's framework provides the overarching group-theoretic strategy and the parachute lattice construction as a conceptual tool for demonstrating how multiple cf-IE properties might be simultaneously forced upon a group \(G\) if FLRP has a positive answer.

2. TCT provides a rich vocabulary of algebraic properties (\(P_{\mathrm{alg}}\)) associated with the structure of \(\mathrm{Con}(A_G)\) (which is isomorphic to the lattice interval \(L ≅ [H, G]\)). These properties are based on TCT types, type configurations, solvability, abelianness, and tail conditions.

3. The research objective is to translate these TCT-derived algebraic properties of \(A_G\) into group-theoretic properties (\(P_{\mathrm{grp}}\)​) of \(G\), and then to prove that these \(P_{\mathrm{grp}}\)​ are indeed cf-IE, i.e., enforceable by some lattice.

If a set of such TCT-derived cf-IE group properties, possibly combined with known cf-IE properties (like those from DeMeo's \(L_7\) analysis [1]), can be shown to be mutually incompatible (i.e., their intersection is empty), then Theorem 3.6 (C) would lead to a contradiction, implying FLRP has a negative answer. For example, one might find a TCT-derived property \(P_1\)​ (enforced by lattice \(L_1′\)) implying \(G\) has a highly non-abelian structure, and another \(P_2\) (enforced by \(L_2′\)) implying \(G\) has strong commutativity properties. If \(P_1\) and \(P_2\) are incompatible, then the parachute lattice \(P(L_{\mathrm{any}}, L_1′​, L_2′​)\) would be unrepresentable by any group as a core-free interval, falsifying statement (B) of Pálfy-Pudlák.

A subtle but critical distinction must be maintained: a "forcing lattice" versus an "enforcing lattice." A specific lattice \(L_{\mathrm{target}}\) (e.g., \(L_7\) or a parachute lattice) might, by its structure, force \(A_G\) (where \(L_{\mathrm{target}} ≅ \mathrm{Con}(A_G)\)) to exhibit certain TCT characteristics, which in turn imply a group property \(P_{\mathrm{grp}}\)​ for \(G\). However, for \(P_{\mathrm{grp}}\)​ to be a cf-IE property in DeMeo's sense, there must exist some lattice \(L_{\mathrm{enf}}\) (which could be different from \(L_{\mathrm{target}}\)) such that any group \(X\) representing \(L_{\mathrm{enf}}\) as a core-free interval \([K, X]\) must possess property \(P_{\mathrm{grp}}\)​. This two-layered lattice argumentation is essential for the logical integrity of applying Theorem 3.6. The TCT-derived cf-IE properties are somewhat self-referential in this regard: the "enforcing lattice" \(L_{P_i}\) for a TCT-derived property \(P_i\) would itself need to be a lattice whose structure inherently forces specific TCT features on any algebra whose congruence lattice it is.

DeMeo's analysis of \(L_7\) in [1] already provides a set of potent cf-IE properties (\(G\) is primitive, insoluble, \(C_G(N) = 1\), etc.). If TCT analysis of \(L_7\) (or other lattices) can yield new, independent cf-IE properties of \(G\), the intersection of required properties shrinks, making a contradiction more attainable. For instance, \(L_7\) is non-modular, implying \(\mathrm{Con}(A_G)\) must admit types 1 or 5; if this admission can be translated into a new cf-IE group property not already covered by DeMeo's analysis, progress is made.

Table 2. Known and Candidate TCT-Derived cf-IE Properties. This table outlines existing cf-IE properties and proposes candidate properties derivable from TCT, highlighting the crucial link to group \(G\) and the nature of the enforcing lattice.

Property Type	Property Description (for Group \(G\) or Algebra \(A_G\)≅G/H)	Known/ Candidate	Enforcing Lattice/Condition (Hypothesized for Candidates)	Notes / Connection of \(A_G\) property to \(G\)
DeMeo (Known)	\(G\) is insoluble	Known	Pálfy's lattice LS​ (not representable by soluble groups)	Direct group property.
DeMeo (Known)	\(G\) is not An​ or Sn​ (for any n)	Known	Lattices from Basile, Aschbacher & Shareshian	Direct group property.
DeMeo (Known, via \(L_7\))	\(G\) is subdirectly irreducible	Known if \(L_7 ≅ [H, G]\)	\(L_7\)	Property of \(G\) if \(L_7\) is the interval.
DeMeo (Known, via \(L_7\))	For any \(1 = N ◃ G\), \(C_G(N) = 1\)	Known if \(L_7 ≅ [H, G]\)	\(L_7\)	Property of \(G\) if \(L_7\) is the interval.
TCT-derived (Cand.)	\(V(A_G)\) omits TCT type 1 (is a Taylor variety)	Candidate	A lattice \(L_{no−1}\) whose structure forces any \(\mathrm{Con}(A) ≅ L_{no−1}\) to omit type 1.	Challenge: Translate "\(V(G/H)\) has Taylor term" to a structural property of \(G\). May relate to \(G\) having no "unary-like" actions or specific chief factor properties.
TCT-derived (Cand.)	\(V(A_G)\) omits TCT types {1,5} (satisfies a non-trivial congruence identity)	Candidate	A lattice \(L_{no−1,5}\) whose structure forces omission of types {1, 5}.	Challenge: Translate "\(V(G/H)\) satisfies cong. identity \(X\)" to a property of \(G\).
TCT-derived (Cand.)	\(\mathrm{Con}(A_G)\) contains an N5 sublattice (hence types 1 or 5 must be present in \(V(A_G)\))	Candidate	Any non-modular lattice \(Lₙₘ\).	If \(Lₙₘ ≅ [H, G]\), then \(V(G/H)\) has types 1 or 5. Could force \(G\) to be non-CM (if tails are non-empty) or relate to specific simple sections of \(G\).
TCT-derived (Cand.)	\(\mathrm{Con}(A_G)\) is modular (hence \(V(A_G)\) omits types 1,5 and has empty tails for types {2,3,4})	Candidate	A modular, non-distributive lattice \(Lₘ\).	If \(Lₘ ≅ [H, G]\), \(V(G/H)\) is congruence modular. Strong constraint. May imply \(G\) is solvable or has specific chief factor structures (e.g., only affine or simple non-abelian of specific TCT types).
TCT-derived (Cand.)	An interval \(I[α, β]\) in \(\mathrm{Con}(A_G)\) is solvable (all prime factors type 1 or 2)	Candidate	A lattice \(L\) whose structure forces a specific interval to be solvable in any \(Con(A) ≅ L\).	Forces local structure of \(Con(G/H)\) to be types 1 or 2. \(A_G\) has locally abelian/affine structure. Impact on \(G\)'s derived series or commutator structure?

4.2. Methodological Strengths

The proposed combination of DeMeo's enforceability framework with TCT offers significant methodological advantages. TCT provides a systematic and deeply structural way to analyze \(\mathrm{Con}(A_G)\) (which is isomorphic to the given lattice interval \(L\)). This goes beyond classical lattice theory, offering a classification of local algebraic behaviors (the five types) and rules for how these types are distributed within the congruence lattice (e.g., type preservation under projectivity, constraints imposed by M3 or N5 subconfigurations). [2 (Lemmas 5.19, 6.2--6.6, 6.9, 6.10)]

The connection of TCT types to Malt'sev conditions and congruence identities provides a rich source of strong algebraic constraints on \(A_G\).[6] DeMeo's framework, particularly Theorem 3.6, then provides the crucial linkage from these (potentially new) algebraic properties of \(A_G\) (if they can be translated into group-theoretic terms) to the FLRP itself. The Pálfy-Pudlák theorem, combined with DeMeo's core-free condition, ensures that the TCT analysis of \(L ≅ \mathrm{Con}(A_G)\) is directly relevant to the FLRP.

4.3. Anticipated Hurdles and Challenges

Despite the promise, several substantial hurdles must be overcome.

1. The Translation Problem. The foremost challenge is translating algebraic properties of \(A_G\) (the \(G\)-set \(⟨G/H, ϕ(G)⟩\)), derived from TCT analysis of \(L ≅ \mathrm{Con}(A_G)\), into meaningful and provably cf-IE group-theoretic properties of \(G\). For example, if TCT implies \(A_G\) must have a Taylor term (because \(\mathrm{Con}(A_G)\) omits type 1), it is not immediately clear what specific structural property this imposes on \(G\) itself, nor how to prove that this \(G\)-property is cf-IE by some other lattice. This step requires bridging universal algebra with group theory in a non-trivial way.

2. Proving cf-IE Nature. Even if a candidate group-theoretic property \(P_{\mathrm{grp}}\) is derived from TCT considerations, proving it is cf-IE (i.e., finding a lattice \(L_{\mathrm{enf}}\) that enforces \(P_{\mathrm{grp}}\)​ on any group \(X\) representing \(L_{\mathrm{enf}}\)​ as a core-free interval) is a significant task. In [1] DeMeo provides examples, but each such proof is a research result in its own right.

3. Complexity of TCT: TCT is a highly technical and intricate theory. Correctly applying its full depth to derive robust enforceable properties, and then translating these, requires profound expertise.
4. Demonstrating Empty Intersection: The ultimate goal of finding a collection of cf-IE group properties whose intersection is provably empty remains a grand challenge in group theory. TCT may help identify new candidate properties, but the final proof of an empty intersection is a group-theoretic problem.
5. Group Representability of Enforcing Lattices: For a TCT-derived cf-IE property to be useful in DeMeo's strategy (e.g., [1 (Conjecture 3.1)] regarding a property and its negation ), the lattice \(L_{\mathrm{enf}}\)​ that enforces it must itself be "group representable" (isomorphic to an interval in some group's subgroup lattice). Establishing this for potentially complex lattices arising from TCT considerations may not be straightforward.

The path from the TCT properties of \(\mathrm{Con}(G/H)\) to cf-IE properties of \(G\) is the most critical and least explored part of this proposed strategy. It requires a deep understanding of how the action of \(G\) on \(G/H\) reflects back onto the structure of \(G\) itself, in a way that is conditionable by lattice interval structures.

5. Concluding Analysis and Strategic Recommendations

5.1. Overall Assessment of the Combined Strategy's Promise

The strategy of integrating Tame Congruence Theory with DeMeo's framework of enforceable properties offers a novel and potentially powerful approach to the Finite Lattice Representation Problem. TCT provides a sophisticated lens to analyze the structure of \(\mathrm{Con}(A_G)\) (where \(A_G\) is the algebra whose congruence lattice is isomorphic to the given interval \([H, G]\)), potentially revealing algebraic properties of \(A_G\) that were previously inaccessible. DeMeo's Theorem 3.6 provides a clear pathway: if a collection of cf-IE group properties can be found whose intersection is empty, the FLRP would be negatively resolved. The primary promise of the combined strategy lies in TCT's ability to furnish new candidate algebraic properties of \(A_G\), which, if successfully translated into cf-IE group properties of \(G\), could enrich the set of constraints applicable under Theorem 3.6, thereby increasing the chances of finding such an empty intersection.

The strength of this combined approach is its multi-layered attack, leveraging the Pálfy-Pudlák theorem to connect the abstract lattice problem to group theory, DeMeo's framework to define enforceability within group theory, and TCT to provide deep structural insights into the congruence lattices that bridge these domains.

5.2. Recommendations for Specific Research Directions

To realize the potential of this combined strategy, future research should focus on several key areas:

1. The Translation Problem. This is the most critical research direction. Methodologies need to be developed to rigorously translate TCT-derived properties of the algebra \(A_G = ⟨G/H, ϕ(G)⟩\) (such as omitting specific TCT types, satisfying certain Malt'sev conditions, or having specific local congruence geometries) into well-defined group-theoretic properties of \(G\). This involves understanding how the structure of the \(G\)-set \(G/H\) and its TCT characteristics reflect back onto the intrinsic structure of \(G\).

   • Question. If \(V(A_G)\) is a Taylor variety (omits type 1), what does this imply about the normal subgroup structure, solvability, or permutational properties of \(G\) itself?

   • Question. If \(\mathrm{Con}(A_G)\) is congruence modular (implying \(\mathrm{typ}(V(A_G)) ⊆ {2,3,4}\) and empty tails), what restrictions does this place on \(G\) (e.g., related to \(G\) being solvable, or having specific types of chief factors)?

2. Identifying and Proving cf-IE Nature of TCT-Derived Group Properties. Once a group property \(P_{\mathrm{grp}}\)​ is hypothesized from TCT analysis of \(A_G\), it must be proven to be cf-IE. This requires finding a lattice \(L_{\mathrm{enf}}\)​ such that \(L_{\mathrm{enf}} ​≅ [K, X]\) (\(K\) core-free) implies \(X ⊨ P_{\mathrm{grp}}\)​. This may involve constructing specific lattices whose structure inherently forces the desired TCT behavior on any algebra representing them, which in turn forces \(P_{\mathrm{grp}}\)​.

3. Exploiting Geometric Constraints in Labeled Congruence Lattices. A systematic investigation into how specific lattice configurations (e.g., M3, N5, more complex patterns of perspectivity or projectivity within \(L ≅ \mathrm{Con}(A_G)\)) force particular TCT type assignments or type omissions is needed. The rules from Hobby & McKenzie's Chapter 6 on labeled congruence lattices are foundational here.[2]

   • Question. If a lattice \(L\) contains projective prime quotients \(I_1\) and \(I_2\), TCT implies \(\mathrm{typ}(I_1) = \mathrm{typ}(I_2)\) (under suitable conditions). Can this type equality, for specific types forced by \(L\)'s structure, be translated into a cf-IE property of \(G\)?

4. Re-analysis of Critical Lattices (e.g., \(L_7\)). Apply a full TCT analysis to lattices like \(L_7\). DeMeo's analysis of \(L_7\) derived several cf-IE properties.[1] TCT might reveal further constraints on \(\mathrm{Con}(A_G) ≅ L_7\) (e.g., specific type occurrences due to its non-modularity or M3 sublattices) which could translate into additional cf-IE properties of \(G\), potentially strengthening the argument for \(L_7\)'s non-representability or leading to a contradiction.

5. Investigating the "Empty Tails" Condition. The property that "\(A_G\) has only empty-tailed minimal sets (for certain types)" is a strong structural condition linked to congruence modularity.3 Research should explore if this condition, or aspects of it, can be translated into a cf-IE group property.

6. Commutator Theory and TCT Types. The relationship between solvable/abelian congruence quotients (defined via the commutator) and TCT types 1 and 2 is well-established.[2] If a lattice \(L\) forces certain commutator-theoretic properties on \(\mathrm{Con}(A_G)\), this implies restrictions on types 1 and 2. This could lead to cf-IE properties related to the derived series or nilpotency class of \(G\).

Progress in these directions, particularly in systematically bridging the gap between TCT properties of \(A_G\) and cf-IE properties of \(G\), holds the most promise for leveraging this combined strategy to make significant advancements on the Finite Lattice Representation Problem. A "negative" TCT result, such as identifying a TCT type-labeling pattern that is impossible for any finite congruence lattice, could also be impactful if a group interval representation were shown to necessitate such a pattern.

Works cited

1. Interval Enforceable Properties of Finite Groups, William DeMeo, 2012; arXiv: 1205.1927v3.
2. The Structure of Finite Algebras by David Hobby and Ralph McKenzie, accessed May 26, 2025, https://math.hawaii.edu/\~ralph/Classes/619/HobbyMcKenzie-FiniteAlgebras.pdf
3. MODULARITY PREVENTS TAILS 1. Introduction Tame congruence theory is a framework developed to study the local polynomial structur, accessed May 26, 2025, https://www.ams.org/journals/proc/1999-127-01/S0002-9939-99-04882-0/S0002-9939-99-04882-0.pdf
4. (PDF) Algebraic Model Theory - ResearchGate, accessed May 26, 2025, https://www.researchgate.net/publication/245346555_Algebraic_Model_Theory
5. Minimal algebra - Wikipedia, accessed May 26, 2025, https://en.wikipedia.org/wiki/Minimal_algebra
6. math.hawaii.edu, accessed May 26, 2025, https://math.hawaii.edu/\~ralph/Classes/619/OmittingTypesMaltsev.pdf
7. Characterizations of several Maltsev Conditions - Durham Research Online, accessed May 26, 2025, https://durham-repository.worktribe.com/OutputFile/1362095
8. MALTSEV CONDITIONS FOR GENERAL CONGRUENCE MEET-SEMIDISTRIBUTIVE ALGEBRAS • idempotence - Cambridge University Press, accessed May 26, 2025, https://www.cambridge.org/core/services/aop-cambridge-core/content/view/F5754B556BE5AE35852849394371CD9B/S0022481221000141a.pdf/maltsev_conditions_for_general_congruence_meetsemidistributive_algebras.pdf
9. MALTSEV CONDITIONS FOR GENERAL CONGRUENCE MEET-SEMIDISTRIBUTIVE ALGEBRAS • idempotence - ULB : Dok, accessed May 26, 2025, https://ulb-dok.uibk.ac.at/download/pdf/7184498.pdf
10. arXiv:2011.07879v1 [math.LO] 16 Nov 2020, accessed May 26, 2025, https://arxiv.org/pdf/2011.07879
11. math.colorado.edu, accessed May 26, 2025, https://math.colorado.edu/\~kearnes/Papers/kkv1fin.pdf
12. math.hawaii.edu, accessed May 26, 2025, https://math.hawaii.edu/\~ralph/Commutator/comm.pdf
13. a guide for mortals to tame congruence theory, accessed May 26, 2025, https://www.math.u-szeged.hu/\~mmaroti/okt/2008o/writeup.pdf
14. accessed December 31, 1969, https://math.hawaii.edu/\~jb/math616s01/tct_notes.pdf
15. arxiv.org, accessed May 26, 2025, https://arxiv.org/pdf/math/9609219
16. (PDF) An Easy Way to Minimal Algebras - ResearchGate, accessed May 26, 2025, https://www.researchgate.net/publication/228667296_An_Easy_Way_to_Minimal_Algebras
17. Congruence lattices of finite algebras and intervals in subgroup lattices of finite groups. Pálfy, P.P., Pudlák, P. Algebra Universalis 11(1), 22–27 (1980) doi url.
18. Expansions of finite algebras and their congruence lattices (2012). William DeMeo; arxiv 1205.1106.
19. Congruence lattices of finite algebras. William DeMeo. PhD thesis, University of Hawai’i at Mānoa, Honolulu, HI, May 2012; arxiv 1204.4305.
20. Finite lattice representation problem Wikipedia page; Wikipedia, The Free Encyclopedia. Date retrieved: 28 May 2025 04:54 UTC.